انواع تبدیلات ریاضی در برق
تبدیلات ریاضی مختلفی در مهندسی برق وجود دارد که هدف از استفاده از این تبدیلات ریاضی را می توان بصورت زیر بیان کرد:
۱- مجزا کردن (Decoupled) متغیرها
۲- تسهیل حل معادلات با ضرایب متغیر با زمان
۳- ارجاع متغیرها به یک چارچوب مشترك
مهمترین تبدیلاتی که در مهندسی برق بکار می رود عبارت اند از:
۱- تبدیل مولفه های متقارن فورتسکیو (Fortescue symmetrical components)
۲- تبدیل کلارک (Clarke)
۳- تبدیل کنکوردیا (Concordia)
۴- تبدیل پارک (Park)
تبدیل فورتسکیو:
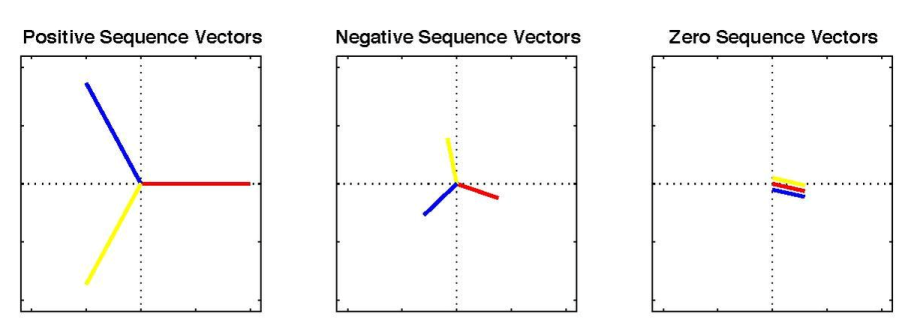
از این تبدیل براي مطالعه شرایط نامتعادل در سیستم هاي قدرت و اجزای آن نظیر ژنراتورها، ترانسفورماتورها و موتورهاي الکتریکی استفاده می شود. طبق نظریه فورتسکیو می توان یک سیستم n فازه نامتقارن را به n سیستم n فازه متقارن تبدیل کرد. پس می توان یک سیستم نامتعادل سه فاز را به سه سیستم متعادل سه فاز تبدیل و محاسبات را در این فضا انجام داد. برای مثال فرض کنید سیستم سه فاز نامتعادل زیر را داشته باشیم:
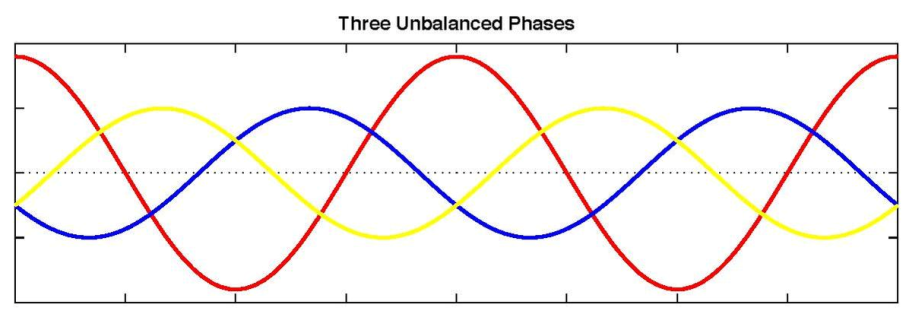 می توان سه سیستم متعادل توالی صفر، توالی مثبت، توالی منفی را صورت زیر رسم کرد:
می توان سه سیستم متعادل توالی صفر، توالی مثبت، توالی منفی را صورت زیر رسم کرد:
معادلات سه توالی بصورت زیر می باشد: 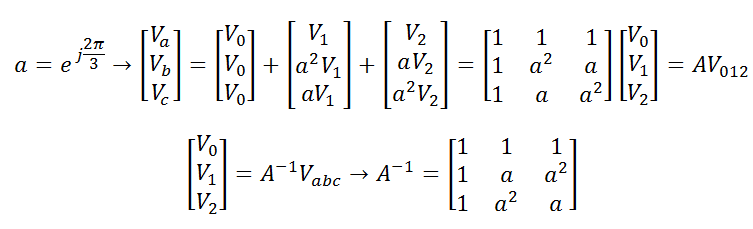
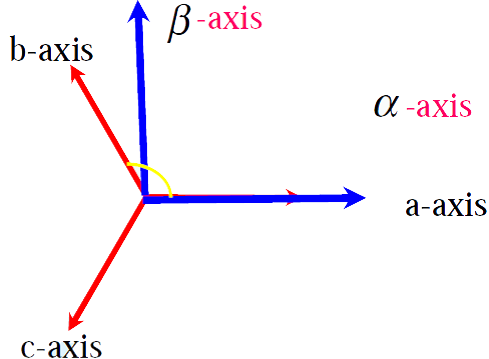
که ماتریس A-1 ماتریس تبدیل فورتسکیو نامیده می شود. تبدیل کلارک سیستم سه فاز زیر و محورهای αβ را بصورت زیر در نظر بگیرید:
می توانیم بوسیلهی تبدیل زیر مولفه های abc را روی محورهای αβ طوری تصویر کنیم که اندازه این مولفه ها در دستگاه جدید ثابت بماند:
این تبدیل را تبدیل کلارک مینامند. توجه کنید که این تبدیل حافظ توان نمیباشد بدین معنی که توان محاسبه شده در سیستم abc با توان محاسبه شده در سیستم αβ متفاوت می باشد. برای مثال سیستم سه فاز متعادل با بار مقاومتی زیر را در نظر بگیرید:
در لحظه ωt=π/2 توان لحظهای بصورت زیر محاسبه می شود:
در لحظه ωt=π/2 توان لحظهای در سیستم αβ بصورت زیر محاسبه می شود:
تبدیل کنکوردیا:
این تبدیل حافظ توان می باشد ولی اندازه مولفه ها در دستگاه αβ تغییر می کند:
برای مثال قبل در لحظه ωt=π/2 توان لحظهای در سیستم αβ بصورت زیر محاسبه می شود:
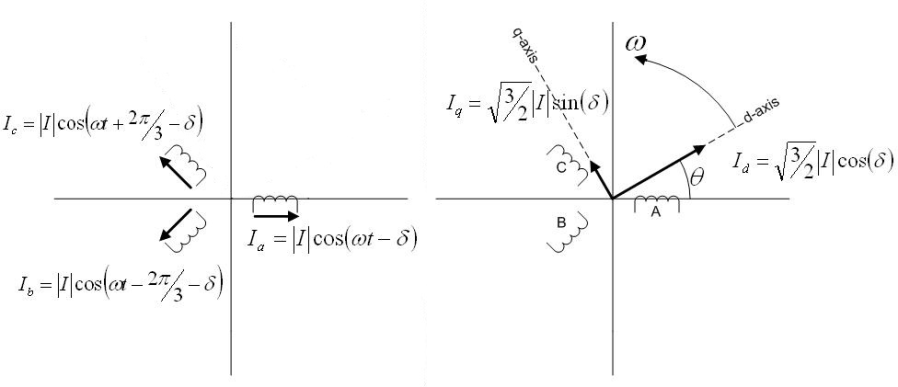
تبدیل پارک:
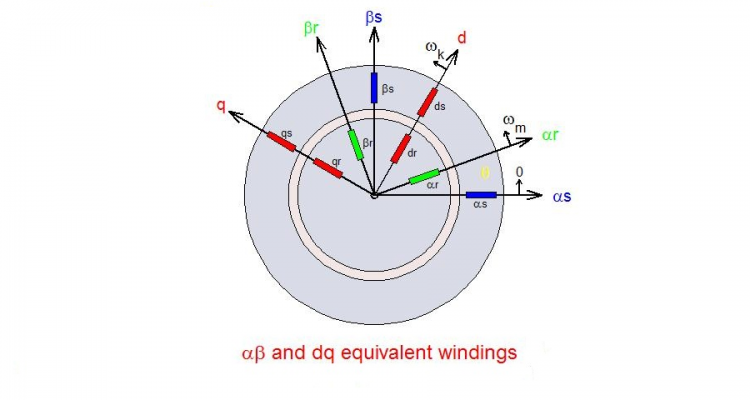
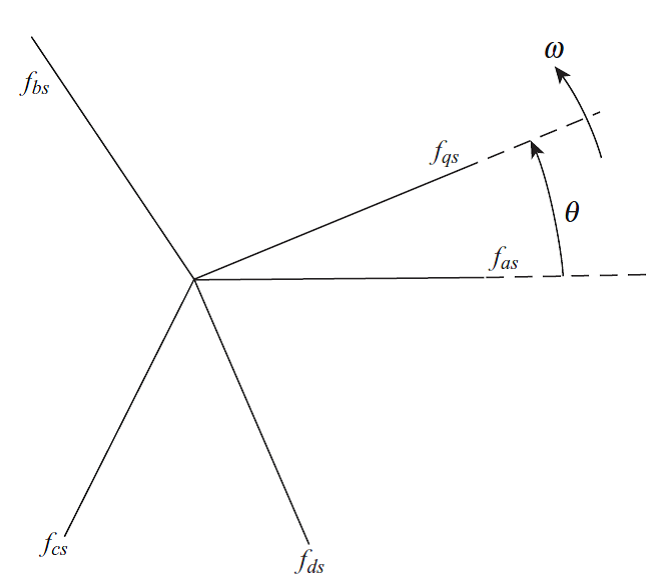
تبدیل پارک یا dqo یک تبدیل ریاضی است که برای ساده سازی تحلیل مدار سه فاز به کار میرود. در حالتی که مدار سه فاز متعادل باشد استفاده از تبدیل dqo سه کمیت متناوب را را به دو کمیت DC کاهش میدهد. میتوان محاسبات ساده شده را روی کمیتهای DC موهومی انجام داد و سپس با استفاده از تبدیل معکوس، نتایج سه فاز AC را بدست آورد. از این تبدیل معمولاً برای ساده سازی تحلیل ماشینهای سه فاز سنکرون یا برای ساده سازی محاسبات کنترل اینورتر استفاده میشود. این تبدیل بر خلاف تبدیل های قبلی مولفه های سیستم ساکن سه فاز abc را روی محورهای سیستم dq که با سرعت ω در حال چرخش می باشد تصویر می کند:
معادلات این تبدیل بصورت زیر است: 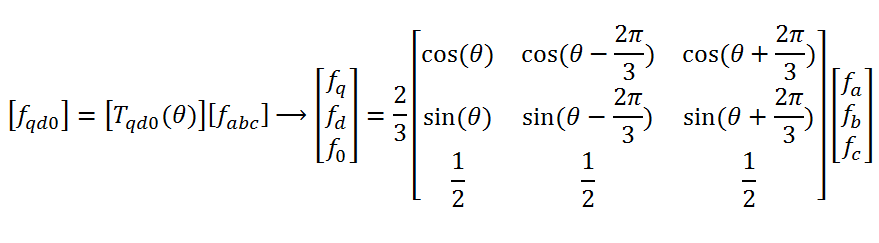
توجه کنید که در این حالت ماتریس تبدیل بصورت تابعی از زاویه θ می باشد و ثابت نیست. می توان سرعت چرخش محور q را دلخواه (سنکرون، غیر سنکرون یا صفر) انتخاب کرد. در تبدیل کلارک اگر مولفه های سیستم سه فاز abc متغیر با زمان باشند پس از انتقال به دستگاه αβ مولفه ها در این دستگاه نیز با زمان تغییر می کند ولی در تبدیل پارک می توان با انتخاب مناسب سرعت چرخش محور dq، مولفه های dq مقدار DC داشته باشند:
از DC شدن این مولفه ها می توان در کنترل موتورهای الکتریکی بصورت زیر استفاده کرد:
1.مجزاسازی جریان های برای کنترل مجزا گشتاور و شار
2.استفاده از کنترل کننده PID بدون در نظر گرفتن ورودی سینوسی
همچنین می توان اثبات کرد که این تبدیل حافظ توان نیست.


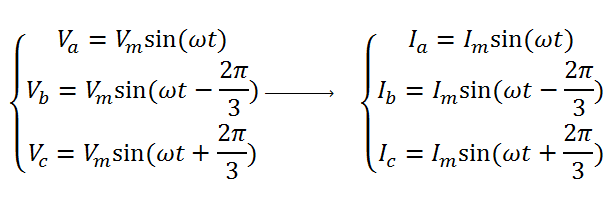
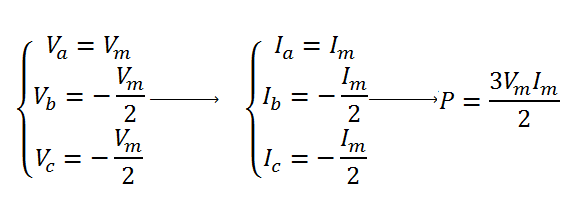
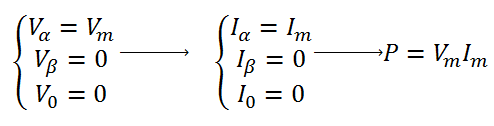
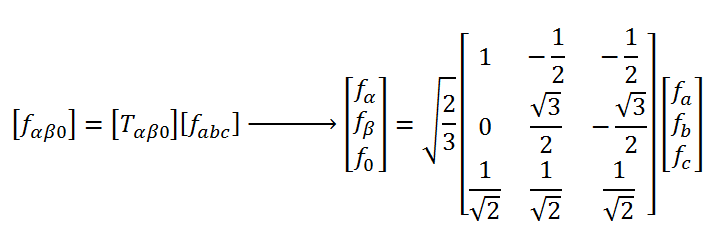
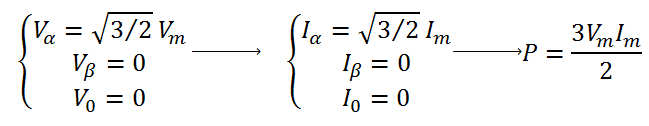




8 Comments
رامین
درباره9 سال agoسلام از مطالب خوب و مفیدتون بسیار سپاسگزارم. در این پست تصویر تبدیل کلارک به درستی آپلود نشده است. لطفا تصحیح بفرمائید. با تشکر
پاسخAdmin
درباره9 سال agoبه دلیل انتقال سایت برخی فایل ها دچار مشکل شده بودند که تصحیح گردید.
باتشکر از اطلاع رسانی شما
پاسخآتنا
درباره8 سال agoبا سلام و عرض وقت بخیر میشه محبت بفرمایید و منابع رو نیز بفرمایید. چون بعید میدونم صرفا از کتاب کراوس باشه. با تشکر
پاسخAdmin
درباره8 سال agoهم از کتاب کراس می باشد و هم از کتاب چی مو اونگ است.
پاسخFAEZE
درباره7 سال agoممنون ، اگه ممکنه اسم خود کتاب رو هم بفرماین و یک سوال دیگه اینکه چرا بعد از اینکه معادلات تبدیل می کنن در قاب dq ، به فضای حالت میبرن ؟ و برای این تیپ مسائل کدوم مرجع رو میفرماین ، ممنون
پاسخAdmin
درباره7 سال agoبه این دلیل معادلات را به فضای حالت می برند که جهت شبیه سازی اگر معادلات بفرم معادلات حالت باشند به راحتی قابل شبیه سازی هستند.
پاسخامیر
درباره6 سال agoسلام. کد شکل 2-10-3 کتاب کراس رو میخوام. باتشکر.
پاسخAdmin
درباره6 سال agoباید از قسمت سفارش پروژه، سفارش بدهید.
پاسخ