مدل موتور القایی در دستگاه DQ
همان طور که گفته شد یکی از مزایای تبدیل dq مجزاسازی پارامترها مدل ماشین می باشد که از این خاصیت می توان برای اعمال استراتژی کنترل برای موتورها استفاده کرد. در این قسمت ابتدا معادلات موتور القایی را بدست آورده و به سمت استاتور منتقل می کنیم. سپس با اعمال تبدیل dq بر روی معادلات، مدل موتور القایی را در دستگاه dq بدست می آوریم.
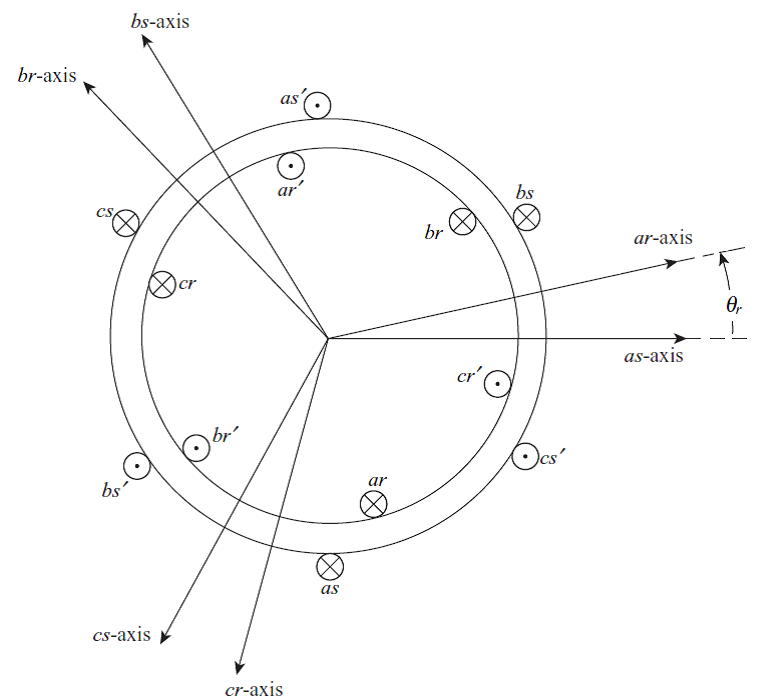
سیم پیچی استاتور و روتور موتور القایی متعادل با توزیع سینوسی را بصورت زیر در نظر بگیرید:
می توان معادله ولتاژ استاتور و روتور را بصورت زیر نوشت:
که اندیس s مربوط به پارامترهای استاتور و r مربوط به پارامترهای روتور می باشد و همچنین ماتریس متغیرها بصورت زیر می باشد:
ماتریس های rs و rr یک ماتریس قطری می باشند. برای سیستم های خطی مغناطیسی، رابطه شار نشتی را بصورت زیر می توان نوشت:
توجه کنید که Ls اندوکتانس نشتی بین سیم پیچی های استاتور، Lr اندوکتانس نشتی بین سیم پیچی های روتور و Lsr اندوکتانس متقابل بین سیم پیچی های استاتور و روتور می باشد. این اندوکتانس ها را می توان بصورت زیر محاسبه کرد:
که Lls و Llr اندوکتانس نشتی و Lms و Lmr اندوکتانس های متقابل می باشند. مثلاٌ چون سیم پیچی فاز a و b با هم 120 درجه اختلاف دارند بنابراین اندوکتانس بین سیم پیچی فاز a استاتور و سیم پیچی فاز b استاتور بصورت زیر می باشد:
همان طور که از ماتریس اندوکتانس متقابل استاتور و روتور مشخص است، این ماتریس به سرعت روتور وابسته است و مولفه های این ماتریس با تغییر سرعت تغییر می کنند.
برای انتقال متغیرهای روتور به طرف استاتور با استفاده از نسبت دور سیم پیچی ها داریم:
چون اندوکتانس مغناطیس کنندگی و متقابل هر دو دارای یک مسیر شار هستند پس می توانیم بنویسیم:
همچنین برای اندوکتانس های روتور داریم:
پس ماتریس اندوکتانس روتور منتقل شده به سمت استاتور بصورت زیر تبدیل می شود:
مقاومت انتقال یافته نیز بصورت زیر محاسبه می شود:
پس روابط ولتاژ منتقل شده به سمت استاتور بصورت زیر تبدیل می شوند:
این مدل یک معادله دیفرانسیل درجه 6 می باشد که ضرایب آن با سرعت روتور تغییر می کند. بنابراین با انتقال این مدل به قاب مرجع dq که با سرعت ω می چرخد ضرایب معادلات دیفرانسیل ثابت می شوند. توجه کنید که سرعت ω یک سرعت دلخواه می باشد و می توان با مساوی قرار دادن آن با سرعت سنکرون، روتور و یا صفر مدل های مختلف موتور القایی را در قاب مرجع های سنکرون، روتور و ساکن بدست آورد.
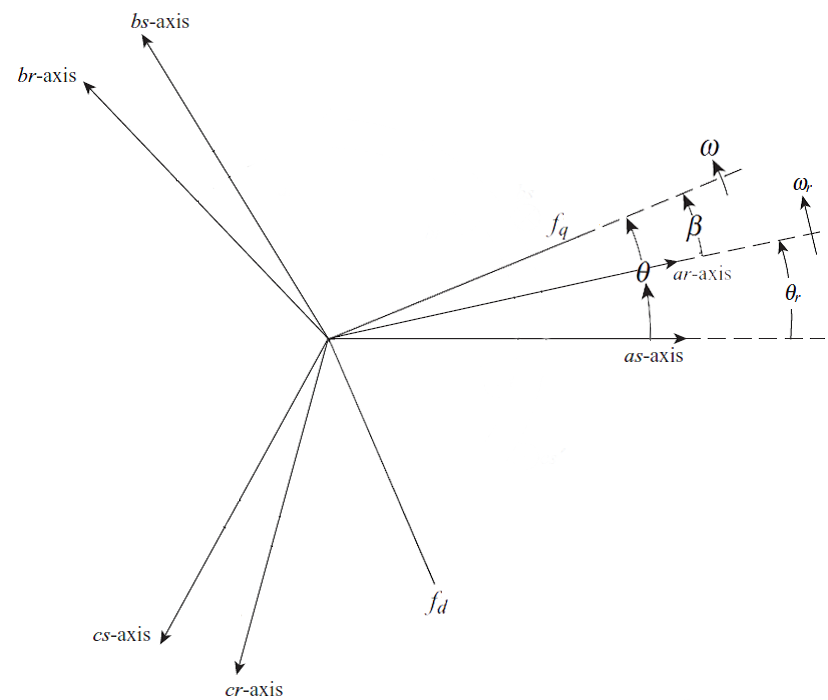
با فرض سرعت دلخواه برای قاب مرجع dq و با توجه به شکل زیر داریم:
با توجه به شکل ماتریس انتقال dq برای انتقال پارامترهای استاتور به قاب مرجع dq عبارت است از:
و ماتریس انتقال dq برای انتقال پارامترهای روتور به قاب مرجع dq عبارت است از:
بنابراین با انتقال معادلات ولتاژ بدست آمده در بالا داریم:
با ساده سازی روابط، معادلات ولتاژ در قاب مرجع dq بصورت زیر محاسبه می شوند:
که قسمت اول مربوط به ولتاژ اهمی، قسمت دوم مربوط به ولتاژ حرکتی و قسمت سوم مربوط به ولتاژ ترانسفورمری می باشد.
شارهای نشتی نیز بصورت زیر محاسبه می شود:
که هر یک از درایه ها بصورت زیر محاسبه می شود:
باز شده ی ماتریس معادلات ولتاژ dq بصورت زیر می باشد:
که مقادیر شار نشتی بصورت زیر محاسبه می شود:
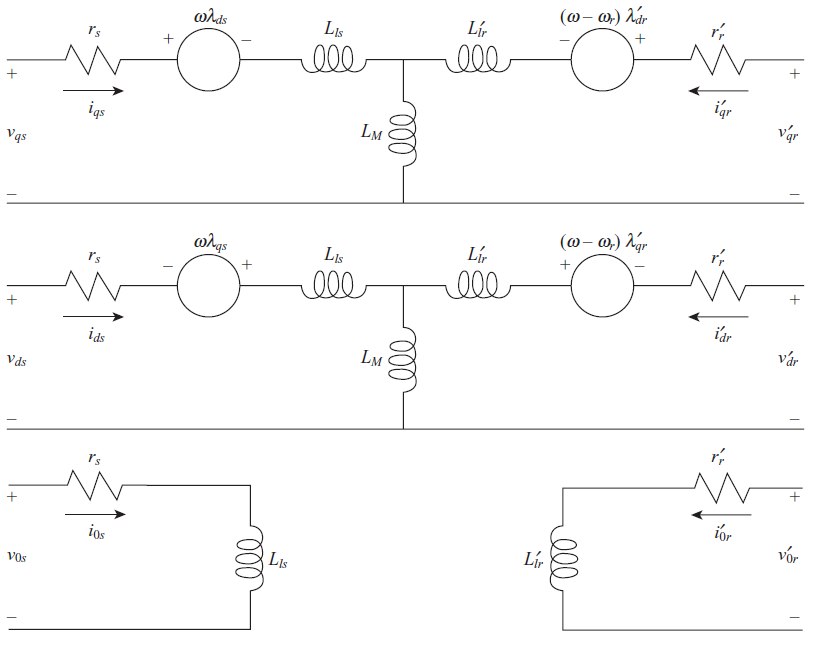
با استفاده از معادلات بالا می توان مدل موتور القایی را بصورت زیر بدست آورد:


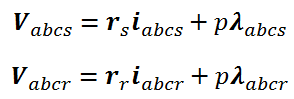
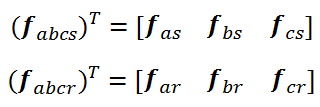
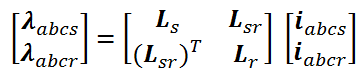
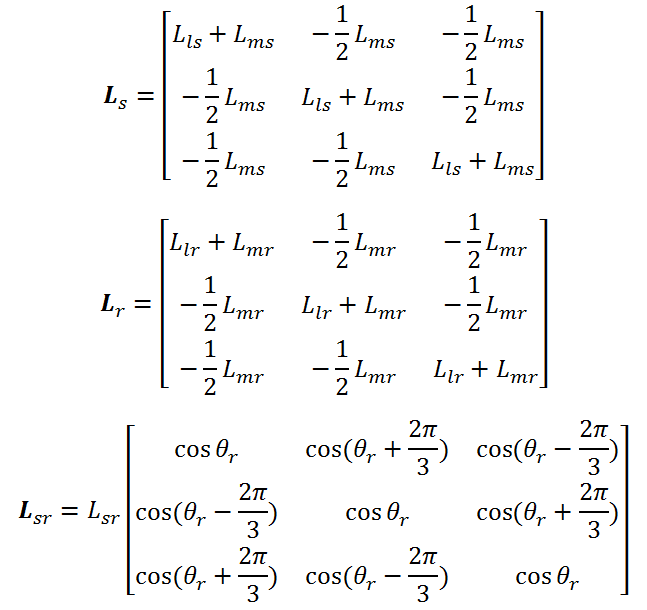
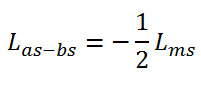
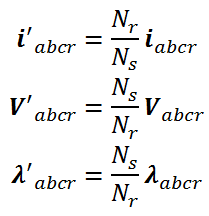
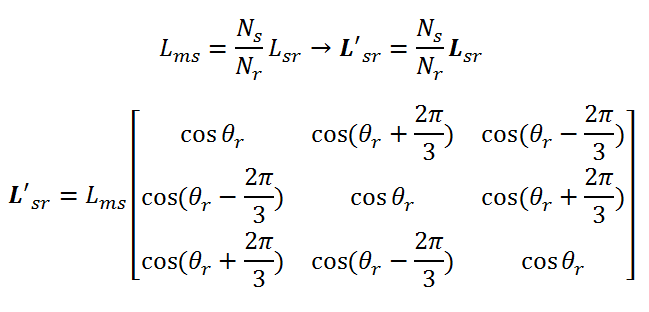

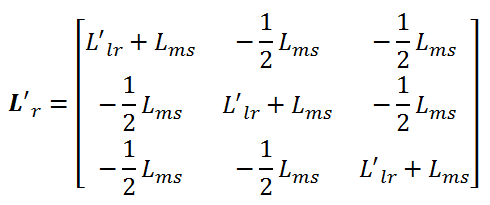
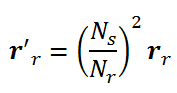
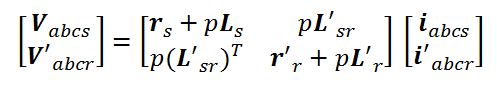
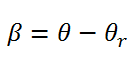
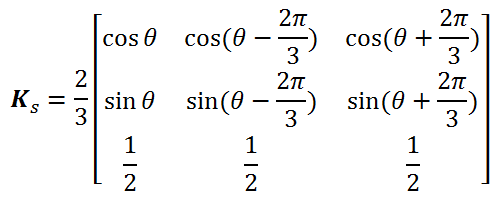
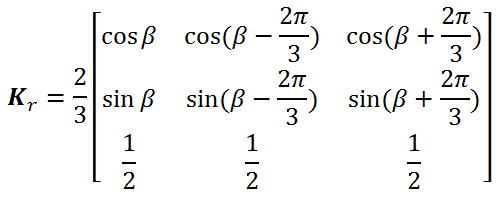
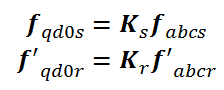
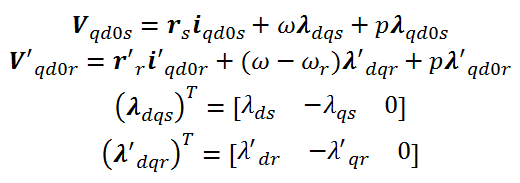
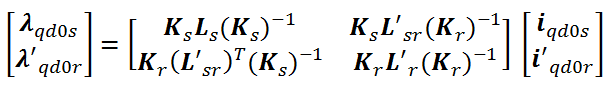
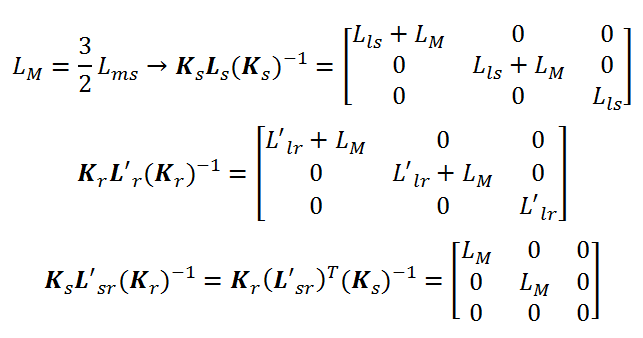

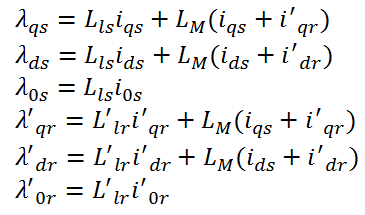




7 Comments
خلیل
درباره10 سال agoخدا خیرتون بده سایتتون واقعا تک،مطالب عالی وکامل همراه با انواع شبیه سازی بدون محدودیت در دسترس!حتی با دسترسی خیلی سریع. بازم میگم خدا خیرتون بده تکین!
پاسخطارق
درباره9 سال agoسلام با تشکر فراوان و با اجازتون چندتا مطلب رو از سایتتون کپی کردم
پاسخAdmin
درباره9 سال agoاشکال ندارد فقط اگر رفرنس بدهید بهتر است.
پاسخایلیا
درباره9 سال agoبا سلام اگر موتور القایی روتور دوبل باشه چطوری باید معادلات رو نوشت؟ شکل نهایی رو نمیشه بدست آورد، تو معادلات آخر روتورها تو هم یه جریانی القا میکنن که نمیشه مدارشو کشید....
پاسخAdmin
درباره9 سال agoباید به مقالات مرتبط مراجعه کنید.
پاسخعلی
درباره7 سال agoبا سلام و تشکر از سایت بسیار مفیدتون در رابطه با این قاب مرجع دی کیو اطلاعات بیشتری می خواستم که توسط چه کسی این روش ابدا شده و d و q و 0 ینی چه مخفف چی هستند ممنون.
پاسخAdmin
درباره7 سال agoبهتر است به کتاب تئوری جامع ماشین های الکتریکی نوشته کراس مراجعه کنید.
پاسخ