کنترل کننده PID
در بسياري از فرآيندهاي صنعتي از كنترل كننده تناسبي P يا تناسبي مشتق گير ،PDتناسبيانتگرال گير PI و يا كنترل كننده تناسبي– مشتق گير– انتگرال گير ،PIDبه عنوان ساختاراصلي كنترل كننده استفاده مي شود. هدف از استفاده از حلقه فيدبك و كنترل كننده را می توان بصورت زير خلاصه کرد:
-
پايداري داخلي
-
دنباله روي از فرمان ورودي ((tracking
-
تضعيف اغتشاش
-
كاهش نويز
-
عدم حساسيت به تغييرات فرآيند
جالب است كه تقريبا در كليه فرآيندهاي صنعتي ساختار ساده كنترل كننده PID تمامنيازهاي فوق را برآورده مي سازد. حتي در برخي از موارد كنترل كننده PI نيز كافي است. درحالت كلي مي توان بيان کرد که كنترل كننده PI براي فرآيندهايي كه براي سيستمهايي که بامدل درجه يک تقريب زده مي شوند، كافي است. در برخي موارد كنترل كننده PID كافي نمي باشد. اين موارد را مي توان به صورت زير خلاصه نمود :
-
فرآيندهاي با ديناميك رتبه بالاتر از دو
-
سيستمهاي با تأخير زياد
-
سيستمهاي داراي صفر ناپايدار يا سيستمهاي غير مينيمم فاز
-
حذف فركانسهاي خاص در خروجي (فيلتر ناچ (Notch filter
در این مقاله ساختار یک کنترل کننده PID و اثر هر یک از پارامترهای آن بر پاسخ خروجی بررسی می شود. فرآيند كنترل شده مطابق مدار حلقه بسته زير را در نظر بگيريد:
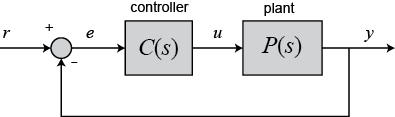
خروجی کنترل کننده PID بصورت زیر می باشد:
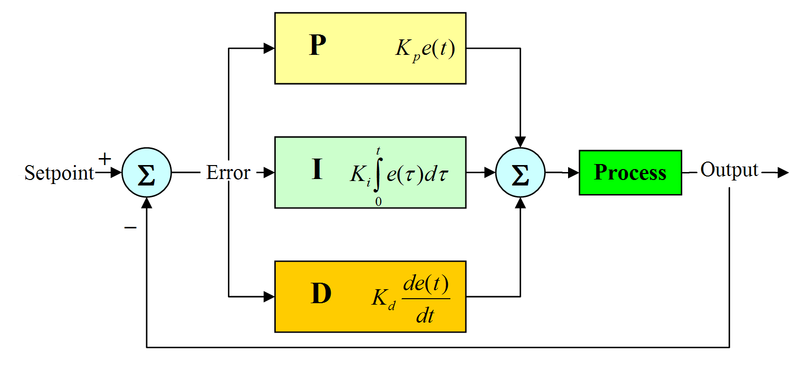
متغییر e که نشان دهنده خطای ردیابی است، تفاوت میان مقدار خواسته شده (r) و مقدار واقعی خروجی(y) می باشد.سیگنال خطا وارد کنترل کننده می شود و مقدار مشتق و انتگرال آن محاسبه می شود و سپس سیگنال کنترلی u با ضریبی از سیگنال خطا (kp)،ضریبی از انتگرال خطا (ki)و ضریبی از مشتق خطا (kd) محاسبه می شود. كنترل كننده PID از جمع سه ترم تشكيل شده است:
- ترم تناسبي : Pكه فرمان كنترل متناسب با ميزان خطا و با بهره kpتقويت مي شود.
- ترم مشتق گير : Dكه فرمان كنترل متناسب با نرخ تغييرات خطا و با بهره kdتقويت مي شود.
- ترم انتگرال گير : Iفرمان كنترل متناسب با انتگرال اين تابع و با بهره kiتقويت مي شود.
تابع انتقال کنترل کننده PID بصورت زیر می باشد:
در نرم افزار Matlab تابع انتقال کنترل کننده را می توان بصورت مستقیم تعریف کرد:
Kp = 1;
Ki = 1;
Kd = 1;
s = tf('s');
C = Kp + Ki/s + Kd*s
همچنین می توان از دستورpid نیز استفاده کرد:
C = pid(Kp,Ki,Kd)
حال اجازه دهيد تاثیر هريك از اين پارامترها را بر پاسخ سیستم توضيح دهیم. بهره تناسبی (kp) باعث کاهش زمان rise time شده ولی خطای دائم را از بین نمی برد. بهره انتگرال گیر (ki) خطای دائم را به ازای ورودی پله از بین می برد ولی باعث کند شدن پاسخ سیستم می شود. بهره مشتق گیر (kd) باعث کم شدن overshoot ، افزایش پایداری و همچنین سریعتر شدن پاسخ سیستم می شود. تاثیر هریک از پارامترهای کنترل کننده را بصورت خلاصه در جدول زیر می توان مشاهده کرد:
|
CL RESPONSE |
RISE TIME |
OVERSHOOT |
SETTLING TIME |
S-S ERROR |
|
Kp |
Decrease |
Increase |
Small Change |
Decrease |
|
Ki |
Decrease |
Increase |
Increase |
Eliminate |
|
Kd |
Small Change |
Decrease | Decrease |
No Change |
مثال: فرض کنید تابع انتقالی بصورت زیر داشته باشیم:
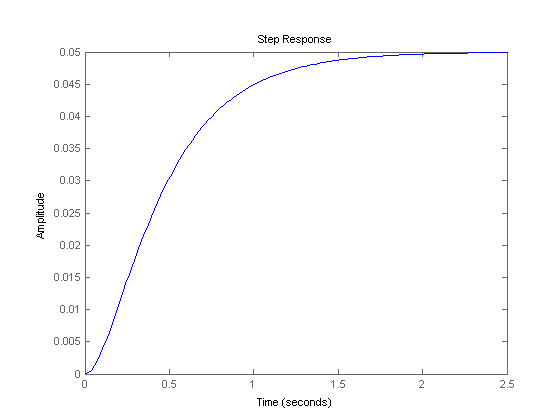
با دستور زیر پاسخ حلقه باز سیستم را به ورودی پله رسم می کنیم:
s = tf('s');
P = 1/(s^2 + 10*s + 20);
step(P)
همان طور که مشخص است، خطای حالت دائم 0.95 و همچنین سیستم بسیار کند است.
کنترل کننده تناسبی:
همان طور که جدول بالا نشان می دهد، ترم تناسبی باعث کاهش rise time، افزایش overshoot و کاهش خطای حالت دائم می شود.تابع انتقال حلقه بسته سیستم بالا با ترم تناسبی بصورت زیر است:
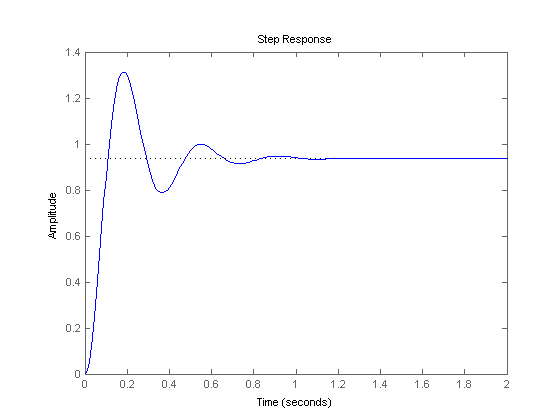
با قرار دادن ترم تناسبی برابر 300 با دستور زیر پاسخ حلقه بسته سیستم را به ورودی پله رسم می کنیم:
Kp = 300; C = pid(Kp) T = feedback(C*P,1) t = 0:0.01:2; step(T,t)
همان طور که شکل بالا نشان می دهد، ترم تناسبی باعث کاهش rise time، افزایش overshoot و کاهش خطای حالت دائم شده است.
کنترل کننده تناسبی- مشتق گیر:
حال بیایید نگاهی به کنترل کننده PD بیاندازیم.همان طور که دیدیم ترم مشتق گیر باعث کاهش overshoot و همچنین settling time می شود. تابع انتقال حلقه بسته سیستم بالا با ترم PD بصورت زیر است:
با قرار دادن ترم تناسبی برابر 300 و ترم مشتق گیر برابر 10 با دستور زیر پاسخ حلقه بسته سیستم را به ورودی پله رسم می کنیم:
Kp = 300; Kd = 10; C = pid(Kp,0,Kd) T = feedback(C*P,1) t = 0:0.01:2; step(T,t)
همان طور که مشخص است ترم مشتق گیر باعث کاهش overshoot و همچنین settling time شده است و همچنین تاثیر کمی بر rise time و خطای حالت دائم داشته است.
کنترل کننده تناسبی-انتگرال گیر- مشتق گیر:
تابع انتقال حلقه بسته سیستم بالا با ترم PID بصورت زیر است:
بعد از چند بار سعی و خطا مقادیر زیر برای پاسخ مناسب در نظر گرفته شد:
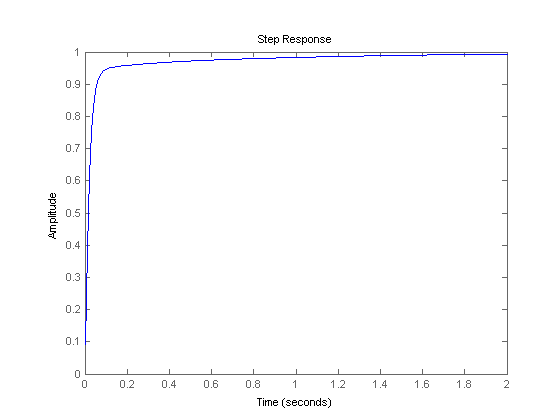
Kp = 350; Ki = 300; Kd = 50; C = pid(Kp,Ki,Kd) T = feedback(C*P,1); t = 0:0.01:2; step(T,t)
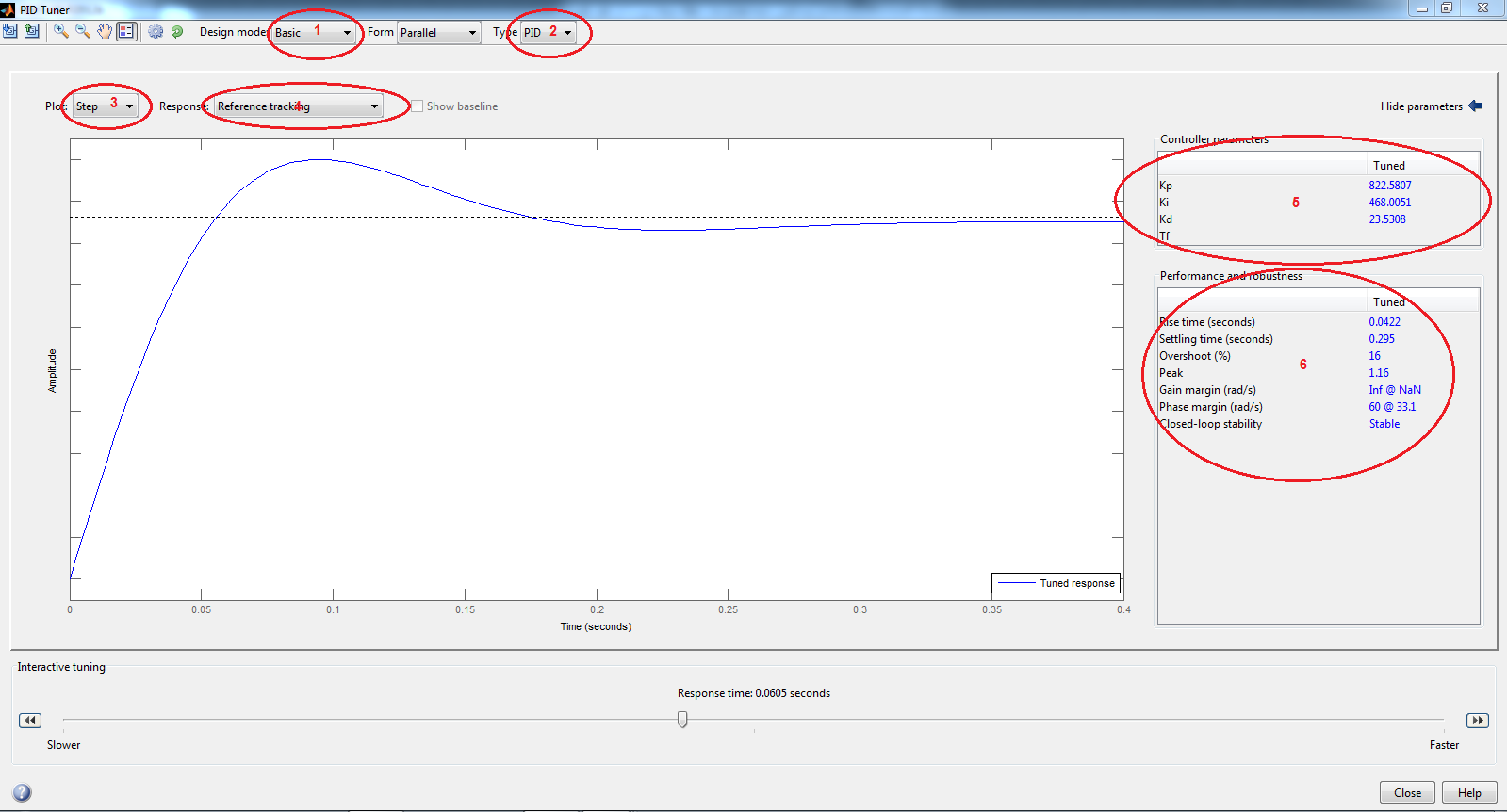
همان طور که مشخص است پاسخ هیچ overshoot و خطای حالت دائمی ندارد و همچنین دارای rise time سریعی می باشد. نرم افزار Matlab دارای ابزاری بنام pidtool می باشد که خیلی راحت می توان یک کنترل کننده PID را بصورت گرافیکی تنظیم کرد.با دستور زیر که پارامتر اول آن تابع انتقال سیستم و پارامتر دوم نوع کنترل کننده را مشخص می کند،می توان وارد محیط PID Tuner شد:
pidtool(P,C)
1)در این قسمت نوع طراحی مشخص می شود(براساس زمان پاسخ یا بر اساس پهنای باند و…)
2)در این قسمت نوع کنترل کننده مشخص می شود.
3)در این قسمت نمایش پاسخ در محدوده زمان یا در محدوده فرکانس(Bode) مشخص می شود.
4)در این قسمت منحنی انتخاب می شود.
5)در این قسمت مقادیر پارامترهای کنترل کننده مشخص می شود.
6)در این قسمت مشخصات پاسخ دیده می شود.(مقدار overshoot،rise time و…)

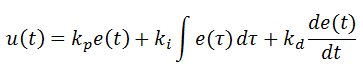
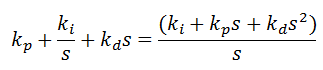
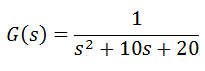
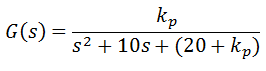
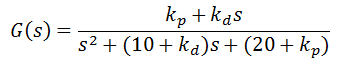

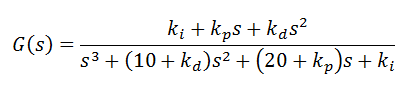




7 Comments
سعيد
درباره10 سال agoاينوميشه بگيد برا موتورالقايي چجوري ميشه وg(s)چي ميشه؟
پاسخAdmin
درباره10 سال agoموتور القایی یک سیستم غیر خطی است و تابع انتقال برای آن تعریف نمی شود.
پاسخعلی
درباره9 سال agoممنون بابت مطلب مفیدتون فقط ی سوال داشتم... من میخوام موضوع پایان نامم رو ک در رابطه با سیستم تاوبری tacan ک یک سامانه موقعیت یاب زمین پایه هست رو قراره این کنترل کننده رو توی این سیستم پیاده سازی کنم...میخواستم راهنماییم کنید که آیا چنین چیزی امکان پذیر هست یا خیر؟
پاسخAdmin
درباره9 سال agoراجع به این سیستم اطلاعی ندارم. اگر بلوک دیاگرام کنترلی آن را ارسال نمایید بررسی می کنم.
پاسخجواد
درباره9 سال agoواقعا ممنون. خیلی خوب توضیح داده اید. موفق باشید.
پاسخعلی
درباره9 سال agoبا سلام در یک مسأله پهنای باند یک کنترلر PI 600 هرتز داده شده است. اما ضرایب تناسبی و انتگرالی آن داده نشده آیا می توان از روی پهنای باند کنترلر، این ضرایب را تعیین نمود؟ چگونه؟
پاسخAdmin
درباره9 سال agoبله اگر پهنای باند سیستم نیز داده شده باشد می توان این مقادیر را نیز تعیین نمود. باید به کتاب Control of Electric Machine Drive Systems - Seung-Ki Sul مراجعه کنید.
پاسخ